
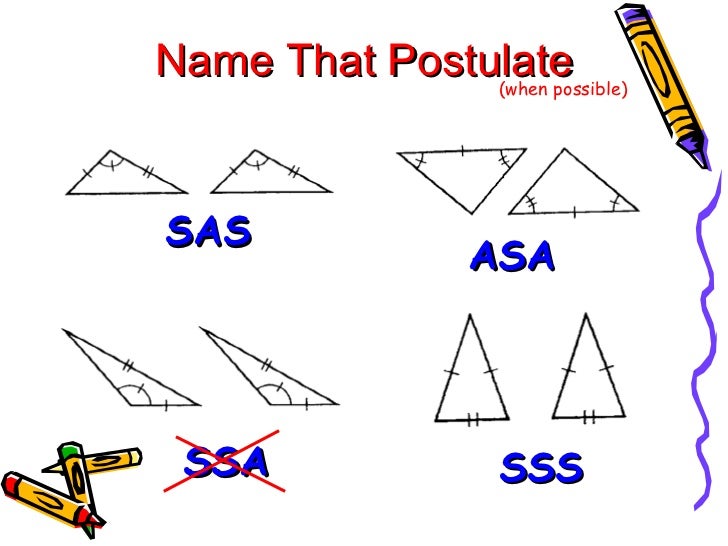
ASA congruence rule states that if two angles and a side in the middle of the two angle are equal, the triangles are congruent.SAS congruence rule states that if two sides and an angle in the middle of the two sides are equal, the two triangles are congruent.SSS congruence rule states that if all sides of a triangle are equal, the triangles are congruent.There are 4 rules to determine if two triangles are congruent: SSS, SAS, ASA, RHS.Congruent triangles are those triangles whose sides and angles are exactly equal.If all the three corresponding sides of two triangles are equal then they are said to be congruent by SSS rule. RHS (Right angle- Hypotenuse-Side)- If the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent.AAS(Angle-Angle-Side)- Two triangles are said to be congruent by AAS condition if their two angles and 1 side are equal.ASA(Angle-Side-Angle)- Two triangles are said to be congruent by ASA condition if their two angles and 1 side are equal. A Triangle Congruence Criterion is a way of proving that two triangles are congruent.SAS(Side-Angle-Side)- Two triangles are said to be congruent by SAS condition if their two sides and 1 angle are equal.

SSS (Side-Side-Side) – Two triangles are said to be congruent by SSS condition if all three sides are equal.WebProving Triangles Congruent Worksheet Answer Key - Quiz Worksheet Sas Asa Sss Triangle lbartman. What is SAS, SSS, ASA, and AAS The four congruence rules of a triangle are: Angle-Angle-Side (AAS): When two angles of a triangle. If there are two triangles A and B then if they fulfil any of the below mentioned conditions then they are said to be congruent and they are mentioned like below: We have AA, SAS, and SSS for similarity of triangles. Whereas the ASA congruence rule states that when two angles with an included side are equal to the two angles along with the included side of another triangle, then these two triangles are said to be congruent. He also shows that AAA is only good for similarity. So, we can say both triangles ABC and PQR are congruent. Sal introduces and justifies the SSS, SAS, ASA and AAS postulates for congruent triangles.


 0 kommentar(er)
0 kommentar(er)
